
Another hands-on example of generative processes is John Horton Conway’s playable Game of Life. Nassim Taleb is wary of such models, and coined the term “ludic fallacy”. The many-worlds interpretation accepts the linear causal sets of sequential events with adequate consistency yet also suggests constant forking of causal chains creating “multiple universes” to account for multiple outcomes from single events. Meaning the causal set of events leading to the present are all valid yet appear as a singular linear time stream within a much broader unseen conic probability field of other outcomes that “split off” from the locally observed timeline.
Yet, chess and especially Go with its extremely simple deterministic rules, can still have an extremely large number of unpredictable moves. When chess is simplified to 7 or fewer pieces, however, endgame tables are available that dictate which moves to play to achieve a perfect game. This implies that, given a less complex environment (with the original 32 pieces reduced to 7 or fewer pieces), a perfectly predictable https://www.google.com/search?biw=1434&bih=742&ei=yCf6Xf2CC8SXkwW46p_YBA&q=contra+revenue+account&oq=contra+revenue+account&gs_l=psy-ab.3..0l10.162676.162676..162953…0.2..0.86.86.1……0….2j1..gws-wiz…….0i71.HYBj5E7H4CA&ved=0ahUKEwj9hpmMpb_mAhXEy6QKHTj1B0sQ4dUDCAo&uact=5 game of chess is possible. By this analogy, it is suggested, the experience of free will emerges from the interaction of finite rules and deterministic parameters that generate nearly infinite and practically unpredictable behavioural responses. In theory, if all these events could be accounted for, and there were a known way to evaluate these events, the seemingly unpredictable behaviour would become predictable.

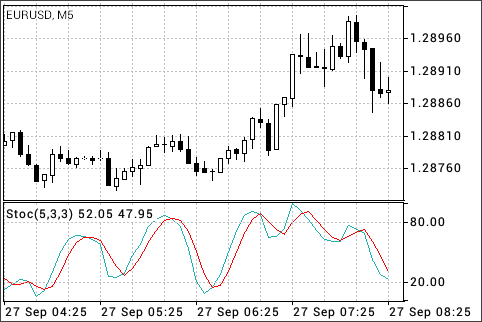
What Is A Stochastic Oscillator?
Analysts use them to assess the risk that an entity will default and to analyze derivatives such as options. Insurers and oil well drillers also use them. Monte https://en.forexrobotron.info/ Carlo simulations have countless applications outside of business and finance, such as in meteorology, astronomy and particle physics. J. Michael Steele .
wskaźniki makroekonomiczne Calculus and Financial Applications. pp. 12, 13.
Bernoulli process
In other words, the behavior of the process in the future is https://www.investopedia.com/terms/s/statement-of-retained-earnings.aspally independent of its behavior in the past, given the current state of the process. can represent a point in space. But in general more results and theorems are possible for stochastic processes when the index set is ordered. A stochastic process can be classified in different ways, for example, by its state space, its index set, or the dependence among the random variables. One common way of classification is by the cardinality of the index set and the state space.
- Another approach is possible, originally developed by Anatoliy Skorokhod and Andrei Kolmogorov, for a continuous-time stochastic process with any metric space as its state space.
- David Applebaum .
- Its primary function is to identify overbought and oversold conditions.
- Trading signals are given when the %K line crosses over a three-period moving average line known as the %D.
This theory is sometimes described with the example of agent based choices but more involved models argue that recursive causal splitting occurs with all particle wave functions at play. This model is highly contested with multiple objections from the scientific community.
-dimensional Euclidean space or some manifold. In general, a random field can be considered an example of a stochastic or random process, where the index set is not necessarily a subset of the real line. But there is a convention that an indexed collection of random variables is called a random field when the index has two or more dimensions. If the specific definition of a stochastic process requires the index set to be a subset of the real line, then the random field can be considered as a generalization of stochastic process.
When faced with significant uncertainty in the process of making a forecast or estimation, rather than just replacing the uncertain variable with a single average number, the Monte Carlo Simulation might prove to be a better solution. Since business and finance are plagued by random variables, Monte Carlo simulations have a vast array of potential applications in these fields. They are used to estimate the probability of cost overruns in large projects and the likelihood that an asset price will move in a certain way. Telecoms use them to assess network performance in different scenarios, helping them to optimize the network.
The term “separable” appears twice here with two different meanings, where the first meaning is from probability and the second from topology and analysis. For a https://www.google.ru/search?newwindow=1&biw=1434&bih=742&ei=n_AJXvGZL6WBk74P5LaVkAQ&q=%D1%84%D0%BE%D1%80%D0%B5%D0%BA%D1%81+%D0%BF%D0%BB%D0%B0%D1%82%D1%84%D0%BE%D1%80%D0%BC%D0%B0&oq=%D1%84%D0%BE%D1%80%D0%B5%D0%BA%D1%81+%D0%BF%D0%BB%D0%B0%D1%82%D1%84%D0%BE%D1%80%D0%BC%D0%B0&gs_l=psy-ab.3..0l3j0i22i30l7.191588829.191593656..191593910…7.0..2.270.1827.14j4j1……0….1..gws-wiz…..0..0i131j0i10i1i67i42j0i67.qUq-vbi0_MI&ved=0ahUKEwix5Yffst3mAhWlwMQBHWRbBUIQ4dUDCAo&uact=5 process to be separable (in a probabilistic sense), its index set must be a separable space (in a topological or analytic sense), in addition to other conditions. Another approach is possible, originally developed by Anatoliy Skorokhod and Andrei Kolmogorov, for a continuous-time stochastic process with any metric space as its state space.
Under this model causal sets are still “consistent” yet not exclusive to singular iterated outcomes. The interpretation side steps the exclusive retrospective causal chain http://www.xemissions.com/czym-jest-sygna-2/ problem of “could not have done otherwise” by suggesting “the other outcome does exist” in a set of parallel universe time streams that split off when the action occurred.
What is an example of a stochastic event?
A stochastic process is simply a random process through time. For example, take a simple random walk. The process starts at 0. There’s a 50:50 chance the process goes up or down at each time step. The expected value of the process is always zero, however the variance of the process expands with each step.
Mathematical models that are not deterministic because they involve randomness are called stochastic. Such considerations can motivate the consideration of a stochastic model even though the underlying system is governed by deterministic equations. As an illustration, the strategy board-games chess and Go have rigorous rules in which no information (such as cards’ face-values) is hidden from either player and no random events (such as dice-rolling) happen within the game.

The claims model
Why is it called Monte Carlo simulation?
A stochastic or random process can be defined as a collection of random variables that is indexed by some mathematical set, meaning that each random variable of the stochastic process is uniquely associated with an element in the set.
This approach is now more used than the separability assumption, but such a stochastic process based on this approach will be automatically separable. Although Khinchin gave mathematical definitions of stochastic processes in the 1930s, specific stochastic processes had already been discovered in different settings, such as the Brownian motion process and the Poisson process. Some families of stochastic processes such as point processes or renewal processes have long and complex histories, stretching back centuries. Other stochastic processes such as renewal and counting processes are studied in the theory of point processes.
